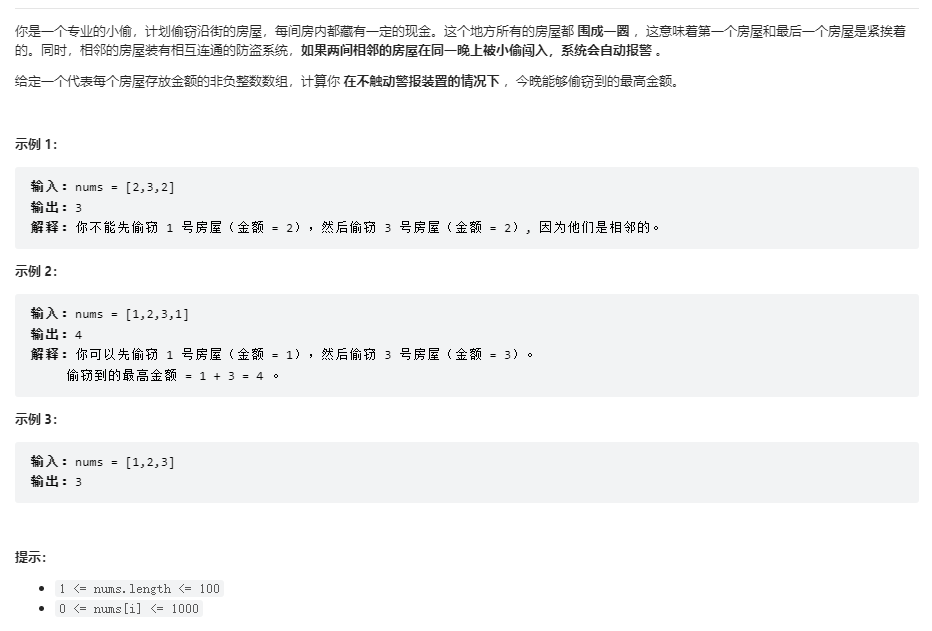
动态规划：打家劫舍 II - 动态规划 - 数据结构与算法 | Aayu Yain = 学无止境 = 世界上大部分事，都没太大意义。真理与热爱除外

# 题目描述

这道题看起来不难，不就在上一道题的基础上添加了首尾房间相邻的限制吗，但我尝试解了三次都失败了，太丢人了 🤣

悄咪咪的看了一下题解，一句关键的话语瞬间就扩展了我的思路

如何才能保证第一间房屋和最后一间房屋不同时偷窃呢？如果偷窃了第一间房屋，则不能偷窃最后一间房屋，因此偷窃房屋的范围是第一间房屋到最后第二间房屋；如果偷窃了最后一间房屋，则不能偷窃第一间房屋，因此偷窃房屋的范围是第二间房屋到最后一间房屋。

原来如此，我之前一直钻在当计算到最后一间房屋的时候，如何知道第一件房间到底是抢了还是没抢，就一直加条件去判断，结果越加越繁琐，繁琐了还不对

看到题解的这句话我就恍然大悟了，我真是笨呐，第一件房和最后一间房不能同时考虑，那我就用两个 for 循环去计算就好啦，三下五除二，五分钟写完，一次性通过～

果然，思路才是最重要的！

	class Solution {
	public:
	int rob(vector<int>& nums) {
	int n = nums.size();
	if (n == 1) return nums[0];
	if (n == 2) return max(nums[0], nums[1]);
	if (n == 3) return max(max(nums[0], nums[1]), nums[2]);
	int prev = 0, curr = nums[0];
	// 先计算排除最后一间房的价格
	for (int i = 1; i < n-1; ++i) {
	int next = max(curr, prev + nums[i]);
	prev = curr;
	curr = next;
	}
	int r1 = curr;
	prev = 0, curr = nums[1];
	// 再计算排除第一间房的价格
	for (int i = 2; i < n; ++i) {
	int next = max(curr, prev + nums[i]);
	prev = curr;
	curr = next;
	}
	return max(r1, curr);
	}
	};