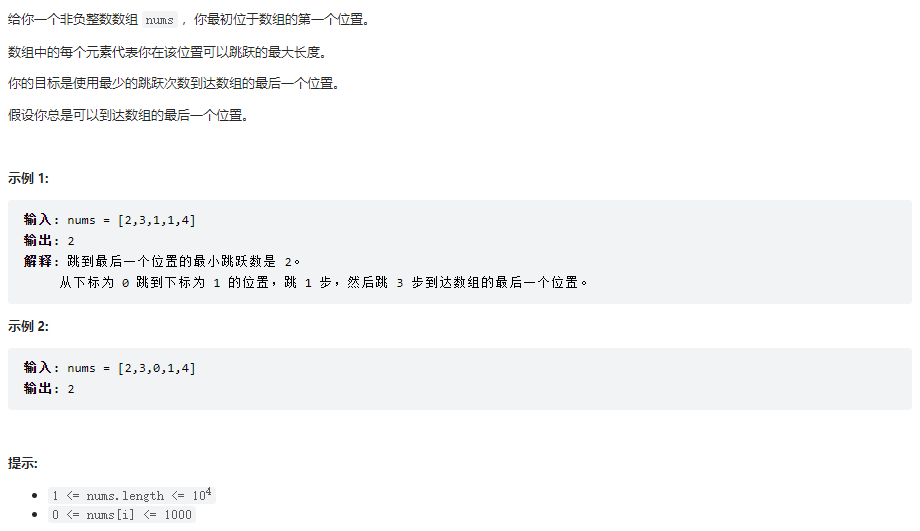
# 题目描述
# 思路与题解
比上一题多加了一些条件,但动态规划的思想不变,都是先求解子问题(小问题),然后逐步求解出一个复杂的问题(大问题)~
上一题我们可以知道在当前 i 处能走到的最大距离,所以稍微一思考,只要后面走的距离在这最大距离之内,步数都不变;只有能走的最大距离不能满足 i 了,才把步数加一,同时更新 i 处能走到的最大距离,是不是很 easy~
class Solution { | |
public: | |
int jump(vector<int>& nums) { | |
int n = nums.size(); | |
if (n < 2) return 0; | |
int limit = nums[0]; | |
int step = 1; | |
int m = limit; | |
for (int i = 1; i < n; ++i) { | |
if (limit < i) { | |
++step; | |
limit = m; | |
} | |
m = max(m, i + nums[i]); | |
} | |
return step; | |
} | |
}; |