# 定义
- 贝叶斯网络是一个
有向无圈图(Directed Acyclic Graph, DAG),由代表变量节点及连接这些节点有向边构成。节点代表随机变量,节点间的有向边代表了节点间的相互关系(由父节点指向其子节点),用条件概率表达变量间依赖关系,没有父节点的用先验概率进行信息表达。 - 令 为定义在 上的一个贝叶斯网络,其联合概率分布可以表示为各个节点的条件概率分布的乘积:
- 其中 为节点 的父节点, 为节点条件概率表。
# 构建贝叶斯网络前的准备
- 我想要解决的问题是什么?
是要进行一般的预测,还是对数据进行解释,还是要对独立条件进行探索。
- 针对我们的问题,尽可能采集到足够多的观测数据,或者是专业知识
- 决定哪些观测数据是值得被建模的
- 把观测数据变成很多取值互斥,却又完全穷尽的变量
这种定义变量取值的方法又叫做 MECE(Mutually Exclusive, Collectively Exhaustive)分析法
# 条件独立性
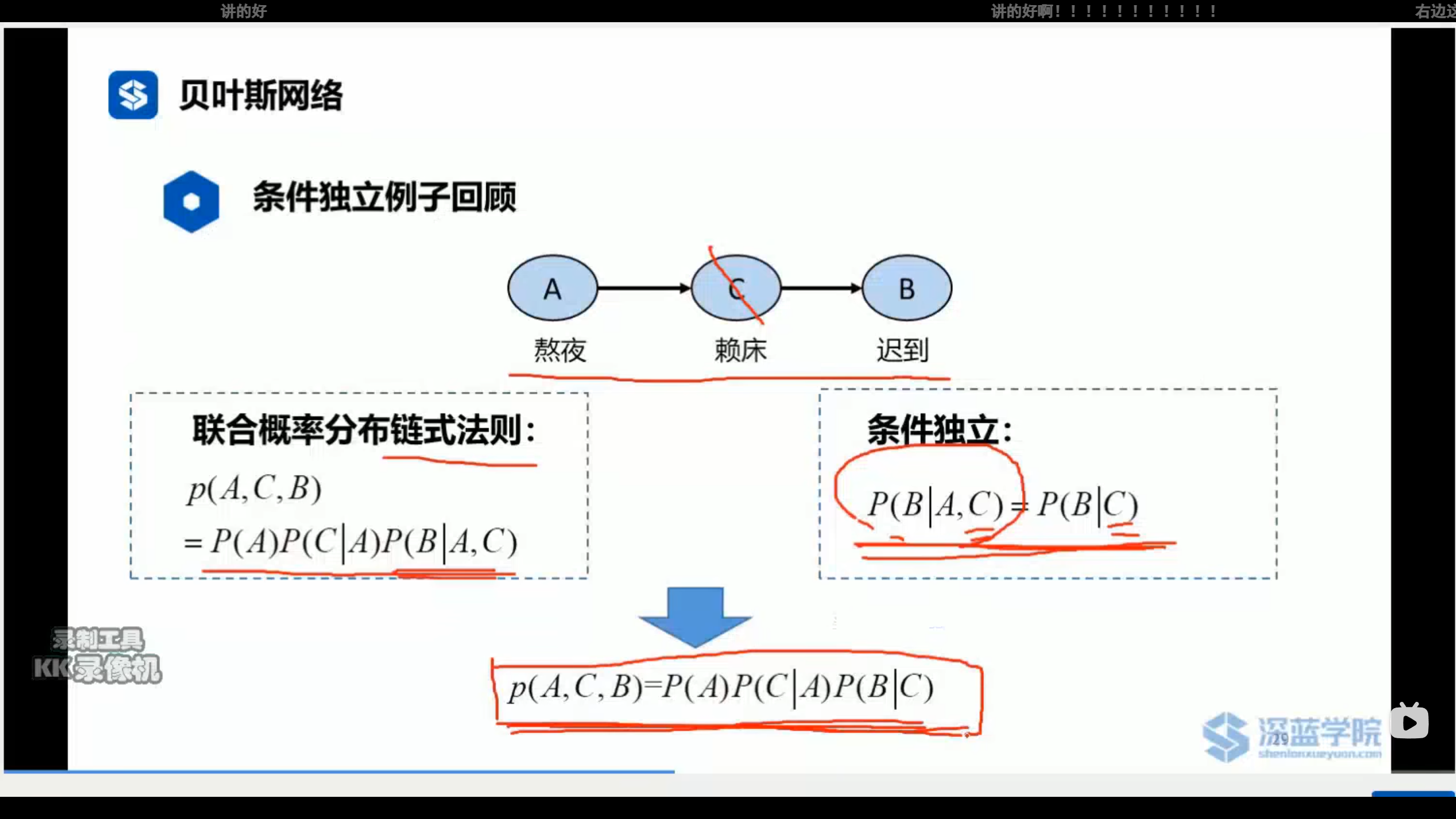
关键之处在于,若已知 C 发生的情况下,B 是否发生与 A 是无关的。因为 A 是影响 C 发生的概率来影响 B,既然 C 已经发生了,B 就和 A 无关。
所以 $$P (B|A,C)=P (B|C)$$
# 参考链接
- 贝叶斯网络基础
- 贝叶斯网络